程序设计#4 SP 接雨水的四种解法
https://leetcode.cn/problems/trapping-rain-water/description/comments/3115811/
孔乙己身材高大,却总带着一副青白的脸色,眼角时常堆积着倦意,一头乱发油腻地贴在额前。他自称拿过ACM银牌,却似乎从未进过大厂,也不懂面试的门道,日子过得颇为落魄。和人交谈时,三句不离“时间复杂度”、“空间复杂度”,总说些让人半懂不懂的话。
有一天,他刚解完一道Hard题目,旁边围观的新人便故意高声嚷道:“孔乙己,你肯定又写暴力解法了!”孔乙己瞪大眼睛道:“你怎么这样凭空污人清白……”“什么清白?我前天亲眼见你写了个O(n²)的解法,被评论区骂得狗血淋头。”孔乙己顿时涨红了脸,额上青筋条条绽出,争辩道:“O(n²)不能算暴力……算法的事,能算暴力么?”接着便是一些难懂的话,什么“约束条件下各有适用”,什么“n很小不必最优”之类,引得众人都哄笑起来:论坛内外充满了快活的空气。
这些时候,我也可以跟着笑,管理员是绝不会责备的。而且管理员一见孔乙己,也每每故意这么问他,逗大家发笑。孔乙己自知无法与他们交流,只好转而找萌新说话。有一回他对我说:“你刷过题吗?”我略一点头。他说:“刷过题……那我考你一考,接雨水这道题,怎么解?”我想,一个刷题刷到这般境地的人,也配考我么?便转过脸去,不再理会。孔乙己等了许久,很恳切地说道:“不会解罢……我教给你,记着!这题该好好记住,将来做了面试官,可用来考人。”我暗想我离面试官还远着呢,再说面试官也一般不考Hot100;既觉得好笑,又不耐烦,便懒懒地回他:“谁要你教,不是双指针秒杀么?”孔乙己显出极高兴的样子,用两个指头的长指甲敲着桌子,点头说:“对呵对呵!……接雨水可有三样解法,你知道么?”我更加不耐烦了,扭头走远。孔乙己刚蘸了酒想在桌上手撕代码,见我怎么也不热心,终于叹一口气,露出极惋惜的表情。
今天不折腾双指针和滑动窗口了,今天弄一个经典的算法题:接雨水。
原题:42. 接雨水 - 力扣(LeetCode) 或者 T574153 接雨水 - 洛谷。
给定
n个非负整数表示每个宽度为1的柱子的高度图(记为height),计算按此排列的柱子,下雨之后能接多少雨水。
先看图:
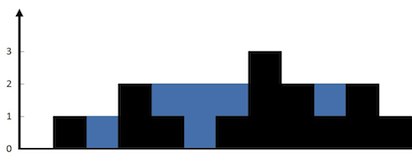
input:
12
0 1 0 2 1 0 1 3 2 1 2 1暴力解法
假设现在遍历到了 height[i],那么从它开始,分别向左向右遍历寻找最高的柱子(记作 left_max 和 right_max),这两个柱子中的较小者减去 height[i] 就是当前柱子的存水量。
换言之,代码表示如下。
int water = std::min(left_max, right_max) - height[i];只要它是一个正数,我们就能直接把它加入总存水量。
int trap_bruteforce(const std::vector<int>& height) {
if (height.size() < 3)
return 0;
int total = 0;
for (int i = 0; i < height.size(); i++) {
int left_max = 0;
for (int j = 0; j < i; j++) {
left_max = std::max(left_max, height[j]);
}
int right_max = 0;
for (int j = i + 1; j < height.size(); j++) {
right_max = std::max(right_max, height[j]);
}
int water = std::min(left_max, right_max) - height[i];
if (water > 0) {
total += water;
}
}
return total;
}(这里没有使用 trap 作为函数名,因为还有其他的方式。)
这样做非常直观,但是时间复杂度是 O(n^2)(每次遍历一个 height[i] 都要遍历完整个数组),最大就能接受 10000 的数据量,它在时间表现上是较劣的。
动态规划预处理
在暴力算法中我们发现,我们重复求了很多次最高的柱子。例如 height[5]、height[6] 和 height[7] 左侧最高的柱子均是 height[4],但是重复求了 3 次。为了避免这种重复的问题,考虑用动态规划的思想求解。
“动态规划”是一个(在我的教程里的)新词,简单地引入一下:
我们先用暴力法想一想:对每个位置
i,都要向左找最高柱子、向右找最高柱子。但你会发现:当我们从
i走到i+1时,“左边最高的柱子”(右边也一样)这件事几乎没有变化,我们在重复做同样的工作。 于是我们可以把这些“会重复出现的中间结果”先算出来保存,后面直接查表使用。这种“把复杂问题拆成一系列更小问题,并把中间结果记下来避免重复计算”的思想,就叫动态规划(Dynamic Programming,DP)。
我们只是简单地进行预处理,但还是有必要说说 DP 的要素。
状态:状态(state)就是用变量表示子问题的解。我们要做的预处理就是求出两个状态数组,记作 left_max 和 right_max。其中 left_max[i] 表示 height[i] 左侧最高柱子的高度(包括它自己),right_max 同理。
无后效性:既然已经求到了 left_max[i],那么无论 left_max[i+1]、left_max[i+2]……的值怎么变,都不会影响 left_max[i]。这样,未来的问题对现在和过去的问题没有任何影响,就叫作无后效性(memorylessness)。
最优子结构:如果我们发现一个问题的最优解,可以由它的子问题的最优解组合而成,我们就说这个问题具有最优子结构(optimal substructure)。也就是如何把子问题组合成大问题。
在这里的问题是:从现在的 height[i] 往左数,最高的柱子在哪里?很显然,要么是之前已经算好的 left_max[i-1],要么是当前的 height[i],也就是:
left_max[i] = std::max(left_max[i-1], height[i]);特别地,当 i == 0,最高的柱子就是 height[0]。同理可得:
right_max[i] = std::max(right_max[i+1], height[i]);重叠子问题:暴力法对每个 i 都重新扫描左侧最大值,这个重新的过程,实际上就是多次解决重叠子问题(overlapping subproblems)。
动态规划只需要解决一次重叠子问题,后面再复用,所以它比暴力法快得多。
状态转移方程:用一个表达式,从已经得到的状态得出当前的状态,这个表达式叫做状态转移方程(State transition equation)。
这里的状态转移方程就是在最优子结构中给出的两个表达式。
left_max[i] = std::max(left_max[i-1], height[i]);
right_max[i] = std::max(right_max[i+1], height[i]);那么就能写出动态规划预处理的函数,剩下的内容和暴力法差别不大。
int trap_dp(const std::vector<int>& height) {
if (height.size() < 3)
return 0;
int n = height.size();
std::vector<int> left_max(n), right_max(n);
int total = 0;
left_max[0] = height[0];
for (int i = 1; i < n; i++) {
left_max[i] = std::max(left_max[i - 1], height[i]);
}
right_max[n - 1] = height[n - 1];
for (int j = n - 2; j >= 0; j--) {
right_max[j] = std::max(right_max[j + 1], height[j]);
}
for (int i = 0; i < n; i++) {
int water = std::min(left_max[i], right_max[i]) - height[i];
if (water > 0) {
total += water;
}
}
return total;
}上面的两种方法在本质上是一样的,只有时间复杂度的区别。动态规划预处理的时间复杂度是 O(n),空间复杂度是 O(n)(开了两个和 height 等大的数组)。
单调栈
单调栈跟前面所提到的单调队列一样,栈中的元素是单调递增或递减的。
这里我们使用单调递减的栈(记作 st)来存储待选的左边墙清单,清单里保持从栈底到栈顶高度递减。这样,只要遇到了一个更高的柱子时,意味着发现了一个可以装水的“山谷”被右墙封住了,可以开始结算积水:
- 底:刚弹出来的那根柱子
st.pop()。 - 左:弹出后新的栈顶
st.top()。 - 右:当前走到的柱子
i。
记得存的是索引,不然无法判断到了哪一个左墙元素。
int trap_stack(const std::vector<int>& height) {
if (height.size() < 3)
return 0;
std::stack<int> st;
int n = height.size();
int total = 0;
for (int i = 0; i < n; i++) {
// 发现了更高的右墙
while (!st.empty() && height[i] > height[st.top()]) {
int bottom = st.top();
st.pop();
if (st.empty()) {
break; // 左侧没有墙了,装不下水
}
int left = st.top();
int width = i - left - 1;
int water = std::min(height[left], height[i]) - height[bottom];
// 当遇到更高的柱子时,我们就会弹出栈顶柱子,计算这个柱子和栈顶柱子之间的水量。
if (water > 0) {
total += water * width;
}
}
st.emplace(i);
}
return total;
}对于测试用例:
5
60 20 20 10 30在碰到索引为 4 的 30 后,栈会相继弹出 10、20 和 20,同时计算储水量,也就是 10 * 1 + 10 * 3 == 40。
容易发现,单调栈实际上是把每一个山谷里的水划分成横向的一层一层,然后计算每一层的水量再求和。
双指针
我们可以设想,用两个指针 l 和 r ,它们相向而行,同时每移动一次,就试着更新当前左/右侧的最高柱子 left_max 和 right_max。
哪边的最高墙更矮(left_max <= right_max),就先结算哪一边。
因为能存的水量取决于 min(left_max, right_max),短板那一边已经确定水位上限了,另一边再高也不影响这一侧。反之亦然。
所以根据之前双指针的知识,就得到了如下代码。
int trap_2pointers(const std::vector<int>& height) {
if (height.size() < 3)
return 0;
int l = 0, r = height.size() - 1;
int left_max = height[l], right_max = height[r];
int total = 0;
while (l < r) {
if (left_max <= right_max) {
l++;
left_max = std::max(height[l], left_max);
total += std::max(0, left_max - height[l]);
} else {
r--;
right_max = std::max(height[r], right_max);
total += std::max(0, right_max - height[r]);
}
}
return total;
}走一个实际的例子看看。
height = [4,2,0,3,2,5]
初始:l=0, r=5,更新得 left_max=4, right_max=5
因为 4 <= 5,结算左侧:4-4=0,l=1
l=1:left_max=4,结算:4-2=2,l=2
l=2:结算:4-0=4,l=3
l=3:结算:4-3=1,l=4
l=4:结算:4-2=2,l=5 停止
总水量:0+2+4+1+2=9右侧一直有高度 5 作为“足够高的挡板”,左侧的水位上限始终由 left_max=4 决定,所以可以一路放心结算左边。
其中,假如 left_max <= right_max,左指针就会开始向右移动,直到 left_max > right_max。反之亦然。
接雨水问题的本质是:每个位置能装多少水,只取决于它左右两边最高柱子的较小值。不同解法的区别只在于:你如何更快地得到“左边最高”和“右边最高”,以及如何把重复计算省掉。
暴力和动态规划预处理的本质是相同的,动态规划是先制作了一张速查表,要查找柱子时只需要查表即可。单调栈解法先把左边的柱子暂时缓存,遇到更高的右边柱子就立刻结算。双指针法因为预先决定好了两边的存水量上限,因此在结算其中一侧时,不会被另一侧影响。